B-tree is a special type of self-balancing search tree in which each node can contain more than one key and can have more than two children. It is a generalized form of the binary search tree.
It is also known as a height-balanced m-way tree.
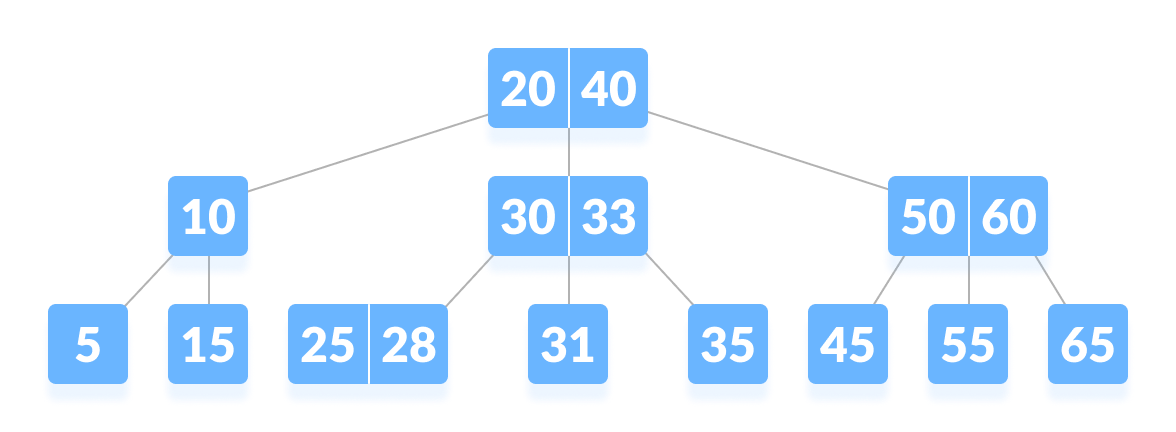
Why do you need a B-tree data structure?
The need for B-tree arose with the rise in the need for lesser time in accessing physical storage media like a hard disk. The secondary storage devices are slower with a larger capacity. There was a need for such types of data structures that minimize the disk access.
Other data structures such as a binary search tree, avl tree, red-black tree, etc can store only one key in one node. If you have to store a large number of keys, then the height of such trees becomes very large, and the access time increases.
However, B-tree can store many keys in a single node and can have multiple child nodes. This decreases the height significantly allowing faster disk accesses.
B-tree Properties
- For each node x, the keys are stored in increasing order.
- In each node, there is a boolean value x.leaf which is true if x is a leaf.
- If n is the order of the tree, each internal node can contain at most n - 1 keys along with a pointer to each child.
- Each node except root can have at most n children and at least n/2 children.
- All leaves have the same depth (i.e. height-h of the tree).
- The root has at least 2 children and contains a minimum of 1 key.
- If n ≥ 1, then for any n-key B-tree of height h and minimum degree
t ≥ 2,h ≥ logt (n+1)/2.
Operations on a B-tree
Searching an element in a B-tree
Searching for an element in a B-tree is the generalized form of searching an element in a Binary Search Tree. The following steps are followed.
- Starting from the root node, compare k with the first key of the node.
Ifk = the first key of the node, return the node and the index. - If
k.leaf = true, return NULL (i.e. not found). - If
k < the first key of the root node, search the left child of this key recursively. - If there is more than one key in the current node and
k > the first key, compare k with the next key in the node.
Ifk < next key, search the left child of this key (ie. k lies in between the first and the second keys).
Else, search the right child of the key. - Repeat steps 1 to 4 until the leaf is reached.
Searching Example
- Let us search key
k = 17in the tree below of degree 3.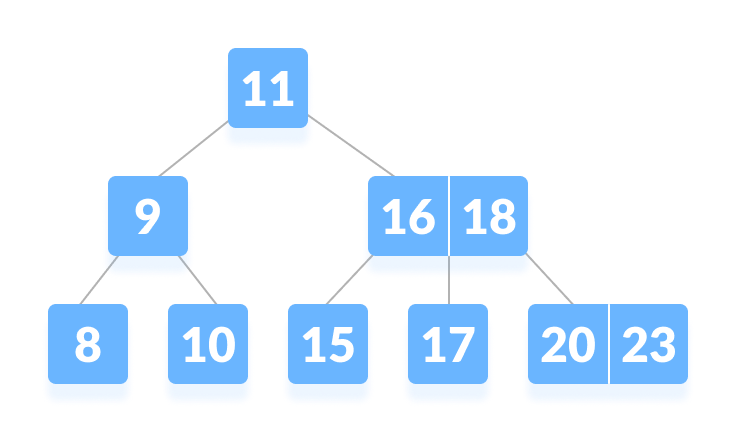
B-tree - k is not found in the root so, compare it with the root key.
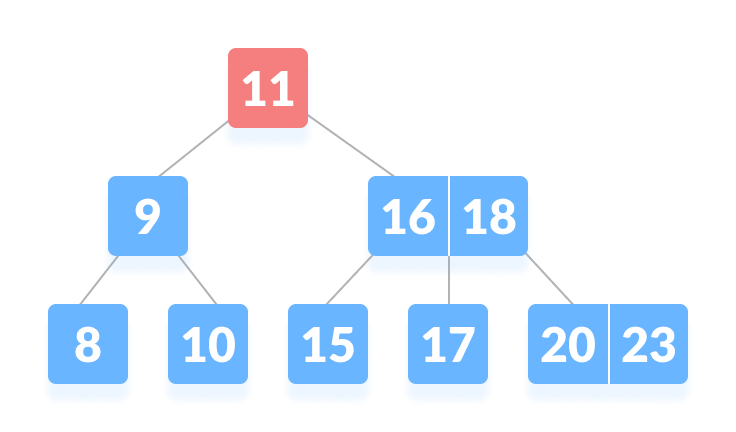
k is not found on the root node - Since
k > 11, go to the right child of the root node.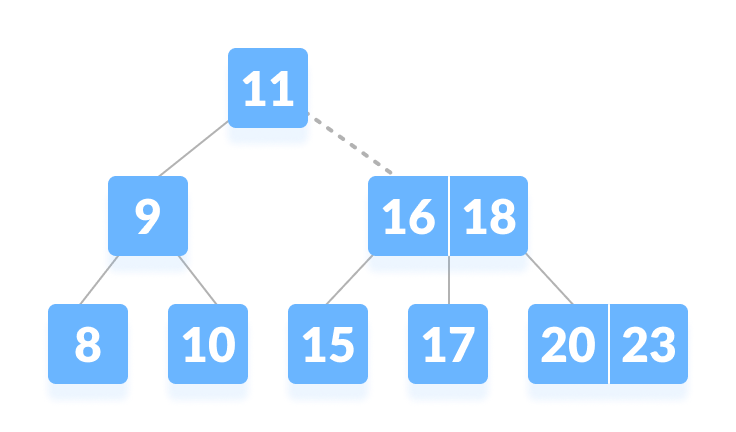
Go to the right subtree - Compare k with 16. Since
k > 16, compare k with the next key 18.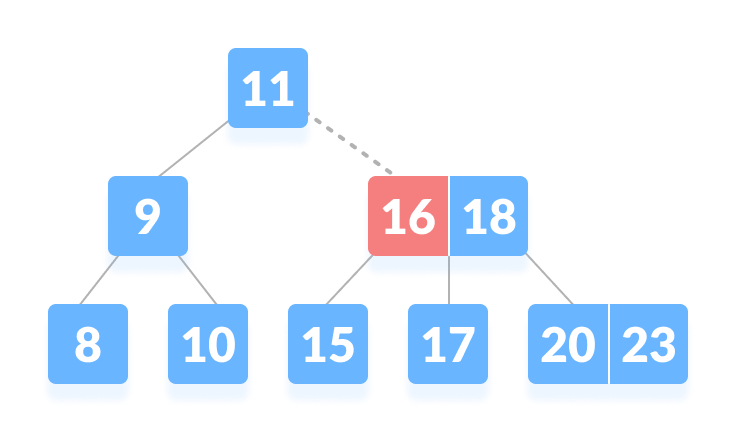
Compare with the keys from left to right - Since
k < 18, k lies between 16 and 18. Search in the right child of 16 or the left child of 18.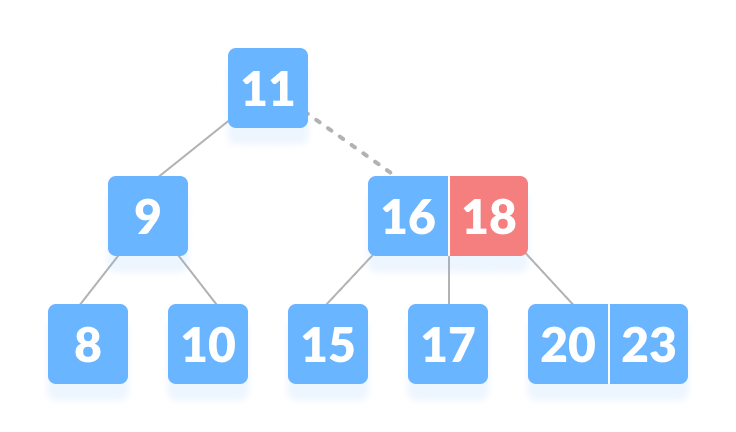
k lies in between 16 and 18 - k is found.
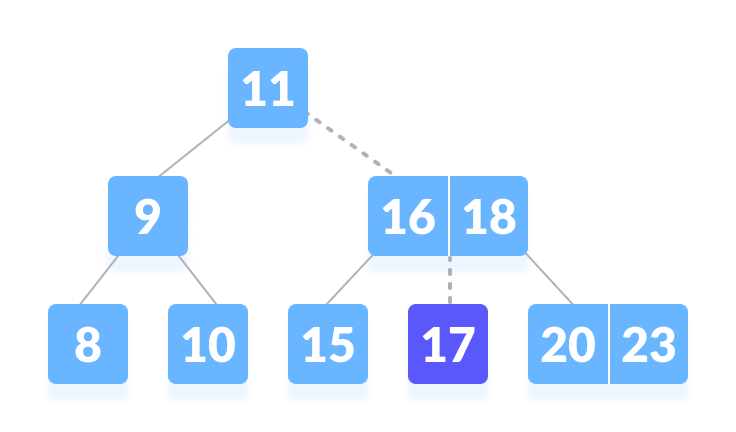
k is found
Algorithm for Searching an Element
BtreeSearch(x, k)
i = 1
while i ≤ n[x] and k ≥ keyi[x] // n[x] means number of keys in x node
do i = i + 1
if i n[x] and k = keyi[x]
then return (x, i)
if leaf [x]
then return NIL
else
return BtreeSearch(ci[x], k)
To learn more about different B-tree operations, please visit
B-tree operations code in Python, Java, and C/C++
# Searching a key on a B-tree in Python
# Create a node
class BTreeNode:
def __init__(self, leaf=False):
self.leaf = leaf
self.keys = []
self.child = []
# Tree
class BTree:
def __init__(self, t):
self.root = BTreeNode(True)
self.t = t
# Insert a key
def insert(self, k):
root = self.root
if len(root.keys) == (2 * self.t) - 1:
temp = BTreeNode()
self.root = temp
temp.child.insert(0, root)
self.split_child(temp, 0)
self.insert_non_full(temp, k)
else:
self.insert_non_full(root, k)
# Insert non full
def insert_non_full(self, x, k):
i = len(x.keys) - 1
if x.leaf:
x.keys.append((None, None))
while i >= 0 and k[0] < x.keys[i][0]:
x.keys[i + 1] = x.keys[i]
i -= 1
x.keys[i + 1] = k
else:
while i >= 0 and k[0] < x.keys[i][0]:
i -= 1
i += 1
if len(x.child[i].keys) == (2 * self.t) - 1:
self.split_child(x, i)
if k[0] > x.keys[i][0]:
i += 1
self.insert_non_full(x.child[i], k)
# Split the child
def split_child(self, x, i):
t = self.t
y = x.child[i]
z = BTreeNode(y.leaf)
x.child.insert(i + 1, z)
x.keys.insert(i, y.keys[t - 1])
z.keys = y.keys[t: (2 * t) - 1]
y.keys = y.keys[0: t - 1]
if not y.leaf:
z.child = y.child[t: 2 * t]
y.child = y.child[0: t]
# Delete a node
def delete(self, x, k):
t = self.t
i = 0
while i < len(x.keys) and k[0] > x.keys[i][0]:
i += 1
if x.leaf:
# Case 1: Node is a leaf
if i < len(x.keys) and x.keys[i][0] == k[0]:
x.keys.pop(i)
return
else:
# Case 2: Key is found in an internal node
if i < len(x.keys) and x.keys[i][0] == k[0]:
return self.delete_internal_node(x, k, i)
# Case 3: Key is not in node, go to the proper child
if len(x.child[i].keys) < t:
self.fill(x, i)
self.delete(x.child[i], k)
def delete_internal_node(self, x, k, i):
t = self.t
# Case 2a: Predecessor has enough keys
if len(x.child[i].keys) >= t:
pred_key = self.get_predecessor(x, i)
x.keys[i] = pred_key
self.delete(x.child[i], pred_key)
# Case 2b: Successor has enough keys
elif len(x.child[i + 1].keys) >= t:
succ_key = self.get_successor(x, i)
x.keys[i] = succ_key
self.delete(x.child[i + 1], succ_key)
# Case 2c: Both children have fewer than t keys
else:
self.merge(x, i)
self.delete(x.child[i], k)
def get_predecessor(self, x, i):
cur = x.child[i]
while not cur.leaf:
cur = cur.child[len(cur.child) - 1]
return cur.keys[len(cur.keys) - 1]
def get_successor(self, x, i):
cur = x.child[i + 1]
while not cur.leaf:
cur = cur.child[0]
return cur.keys[0]
# Merge function to merge two children
def merge(self, x, i):
t = self.t
child = x.child[i]
sibling = x.child[i + 1]
# Merge key from x to child
child.keys.append(x.keys[i])
# Append sibling's keys to child
child.keys.extend(sibling.keys)
# If sibling has children, append them to child
if not child.leaf:
child.child.extend(sibling.child)
# Remove the key from x and delete sibling from child list
x.keys.pop(i)
x.child.pop(i + 1)
# If root becomes empty, reduce the height of the tree
if len(x.keys) == 0:
self.root = child
# Fill function to ensure child has at least t keys
def fill(self, x, i):
t = self.t
# Borrow from the previous sibling
if i != 0 and len(x.child[i - 1].keys) >= t:
self.borrow_from_prev(x, i)
# Borrow from the next sibling
elif i != len(x.child) - 1 and len(x.child[i + 1].keys) >= t:
self.borrow_from_next(x, i)
# Merge with sibling
else:
if i != len(x.child) - 1:
self.merge(x, i)
else:
self.merge(x, i - 1)
def borrow_from_prev(self, x, i):
child = x.child[i]
sibling = x.child[i - 1]
# Move the last key from sibling to x
child.keys.insert(0, x.keys[i - 1])
x.keys[i - 1] = sibling.keys.pop()
# Move the last child of sibling to child if sibling is not a leaf
if not child.leaf:
child.child.insert(0, sibling.child.pop())
def borrow_from_next(self, x, i):
child = x.child[i]
sibling = x.child[i + 1]
# Move the first key from sibling to x
child.keys.append(x.keys[i])
x.keys[i] = sibling.keys.pop(0)
# Move the first child of sibling to child if sibling is not a leaf
if not child.leaf:
child.child.append(sibling.child.pop(0))
# Print the tree
def print_tree(self, x, l=0):
print("Level ", l, " ", len(x.keys), end=":")
for i in x.keys:
print(i, end=" ")
print()
l += 1
if len(x.child) > 0:
for i in x.child:
self.print_tree(i, l)
# Example usage
B = BTree(3)
for i in range(10):
B.insert((i, 2 * i))
B.print_tree(B.root)
B.delete(B.root, (8,))
print("\n")
B.print_tree(B.root)
// Searching a key on a B-tree in Java
public class BTree {
private int T;
// Node creation
public class Node {
int n;
int key[] = new int[2 * T - 1];
Node child[] = new Node[2 * T];
boolean leaf = true;
public int Find(int k) {
for (int i = 0; i < this.n; i++) {
if (this.key[i] == k) {
return i;
}
}
return -1;
};
}
public BTree(int t) {
T = t;
root = new Node();
root.n = 0;
root.leaf = true;
}
private Node root;
// Search key
private Node Search(Node x, int key) {
int i = 0;
if (x == null)
return x;
for (i = 0; i < x.n; i++) {
if (key < x.key[i]) {
break;
}
if (key == x.key[i]) {
return x;
}
}
if (x.leaf) {
return null;
} else {
return Search(x.child[i], key);
}
}
// Splitting the node
private void Split(Node x, int pos, Node y) {
Node z = new Node();
z.leaf = y.leaf;
z.n = T - 1;
for (int j = 0; j < T - 1; j++) {
z.key[j] = y.key[j + T];
}
if (!y.leaf) {
for (int j = 0; j < T; j++) {
z.child[j] = y.child[j + T];
}
}
y.n = T - 1;
for (int j = x.n; j >= pos + 1; j--) {
x.child[j + 1] = x.child[j];
}
x.child[pos + 1] = z;
for (int j = x.n - 1; j >= pos; j--) {
x.key[j + 1] = x.key[j];
}
x.key[pos] = y.key[T - 1];
x.n = x.n + 1;
}
// Inserting a value
public void Insert(final int key) {
Node r = root;
if (r.n == 2 * T - 1) {
Node s = new Node();
root = s;
s.leaf = false;
s.n = 0;
s.child[0] = r;
Split(s, 0, r);
insertValue(s, key);
} else {
insertValue(r, key);
}
}
// Insert the node
final private void insertValue(Node x, int k) {
if (x.leaf) {
int i = 0;
for (i = x.n - 1; i >= 0 && k < x.key[i]; i--) {
x.key[i + 1] = x.key[i];
}
x.key[i + 1] = k;
x.n = x.n + 1;
} else {
int i = 0;
for (i = x.n - 1; i >= 0 && k < x.key[i]; i--) {
}
;
i++;
Node tmp = x.child[i];
if (tmp.n == 2 * T - 1) {
Split(x, i, tmp);
if (k > x.key[i]) {
i++;
}
}
insertValue(x.child[i], k);
}
}
public void Show() {
Show(root);
}
// Display
private void Show(Node x) {
assert (x == null);
for (int i = 0; i < x.n; i++) {
System.out.print(x.key[i] + " ");
}
if (!x.leaf) {
for (int i = 0; i < x.n + 1; i++) {
Show(x.child[i]);
}
}
}
// Check if present
public boolean Contain(int k) {
if (this.Search(root, k) != null) {
return true;
} else {
return false;
}
}
public static void main(String[] args) {
BTree b = new BTree(3);
b.Insert(8);
b.Insert(9);
b.Insert(10);
b.Insert(11);
b.Insert(15);
b.Insert(20);
b.Insert(17);
b.Show();
if (b.Contain(12)) {
System.out.println("\nfound");
} else {
System.out.println("\nnot found");
}
;
}
}
// Searching a key on a B-tree in C
#include <stdio.h>
#include <stdlib.h>
#define MAX 3
#define MIN 2
struct BTreeNode {
int val[MAX + 1], count;
struct BTreeNode *link[MAX + 1];
};
struct BTreeNode *root;
// Create a node
struct BTreeNode *createNode(int val, struct BTreeNode *child) {
struct BTreeNode *newNode;
newNode = (struct BTreeNode *)malloc(sizeof(struct BTreeNode));
newNode->val[1] = val;
newNode->count = 1;
newNode->link[0] = root;
newNode->link[1] = child;
return newNode;
}
// Insert node
void insertNode(int val, int pos, struct BTreeNode *node,
struct BTreeNode *child) {
int j = node->count;
while (j > pos) {
node->val[j + 1] = node->val[j];
node->link[j + 1] = node->link[j];
j--;
}
node->val[j + 1] = val;
node->link[j + 1] = child;
node->count++;
}
// Split node
void splitNode(int val, int *pval, int pos, struct BTreeNode *node,
struct BTreeNode *child, struct BTreeNode **newNode) {
int median, j;
if (pos > MIN)
median = MIN + 1;
else
median = MIN;
*newNode = (struct BTreeNode *)malloc(sizeof(struct BTreeNode));
j = median + 1;
while (j <= MAX) {
(*newNode)->val[j - median] = node->val[j];
(*newNode)->link[j - median] = node->link[j];
j++;
}
node->count = median;
(*newNode)->count = MAX - median;
if (pos <= MIN) {
insertNode(val, pos, node, child);
} else {
insertNode(val, pos - median, *newNode, child);
}
*pval = node->val[node->count];
(*newNode)->link[0] = node->link[node->count];
node->count--;
}
// Set the value
int setValue(int val, int *pval,
struct BTreeNode *node, struct BTreeNode **child) {
int pos;
if (!node) {
*pval = val;
*child = NULL;
return 1;
}
if (val < node->val[1]) {
pos = 0;
} else {
for (pos = node->count;
(val < node->val[pos] && pos > 1); pos--)
;
if (val == node->val[pos]) {
printf("Duplicates are not permitted\n");
return 0;
}
}
if (setValue(val, pval, node->link[pos], child)) {
if (node->count < MAX) {
insertNode(*pval, pos, node, *child);
} else {
splitNode(*pval, pval, pos, node, *child, child);
return 1;
}
}
return 0;
}
// Insert the value
void insert(int val) {
int flag, i;
struct BTreeNode *child;
flag = setValue(val, &i, root, &child);
if (flag)
root = createNode(i, child);
}
// Search node
void search(int val, int *pos, struct BTreeNode *myNode) {
if (!myNode) {
return;
}
if (val < myNode->val[1]) {
*pos = 0;
} else {
for (*pos = myNode->count;
(val < myNode->val[*pos] && *pos > 1); (*pos)--)
;
if (val == myNode->val[*pos]) {
printf("%d is found", val);
return;
}
}
search(val, pos, myNode->link[*pos]);
return;
}
// Traverse then nodes
void traversal(struct BTreeNode *myNode) {
int i;
if (myNode) {
for (i = 0; i < myNode->count; i++) {
traversal(myNode->link[i]);
printf("%d ", myNode->val[i + 1]);
}
traversal(myNode->link[i]);
}
}
int main() {
int val, ch;
insert(8);
insert(9);
insert(10);
insert(11);
insert(15);
insert(16);
insert(17);
insert(18);
insert(20);
insert(23);
traversal(root);
printf("\n");
search(11, &ch, root);
}
// Searching a key on a B-tree in C++
#include <iostream>
using namespace std;
class TreeNode {
int *keys;
int t;
TreeNode **C;
int n;
bool leaf;
public:
TreeNode(int temp, bool bool_leaf);
void insertNonFull(int k);
void splitChild(int i, TreeNode *y);
void traverse();
TreeNode *search(int k);
friend class BTree;
};
class BTree {
TreeNode *root;
int t;
public:
BTree(int temp) {
root = NULL;
t = temp;
}
void traverse() {
if (root != NULL)
root->traverse();
}
TreeNode *search(int k) {
return (root == NULL) ? NULL : root->search(k);
}
void insert(int k);
};
TreeNode::TreeNode(int t1, bool leaf1) {
t = t1;
leaf = leaf1;
keys = new int[2 * t - 1];
C = new TreeNode *[2 * t];
n = 0;
}
void TreeNode::traverse() {
int i;
for (i = 0; i < n; i++) {
if (leaf == false)
C[i]->traverse();
cout << " " << keys[i];
}
if (leaf == false)
C[i]->traverse();
}
TreeNode *TreeNode::search(int k) {
int i = 0;
while (i < n && k > keys[i])
i++;
if (keys[i] == k)
return this;
if (leaf == true)
return NULL;
return C[i]->search(k);
}
void BTree::insert(int k) {
if (root == NULL) {
root = new TreeNode(t, true);
root->keys[0] = k;
root->n = 1;
} else {
if (root->n == 2 * t - 1) {
TreeNode *s = new TreeNode(t, false);
s->C[0] = root;
s->splitChild(0, root);
int i = 0;
if (s->keys[0] < k)
i++;
s->C[i]->insertNonFull(k);
root = s;
} else
root->insertNonFull(k);
}
}
void TreeNode::insertNonFull(int k) {
int i = n - 1;
if (leaf == true) {
while (i >= 0 && keys[i] > k) {
keys[i + 1] = keys[i];
i--;
}
keys[i + 1] = k;
n = n + 1;
} else {
while (i >= 0 && keys[i] > k)
i--;
if (C[i + 1]->n == 2 * t - 1) {
splitChild(i + 1, C[i + 1]);
if (keys[i + 1] < k)
i++;
}
C[i + 1]->insertNonFull(k);
}
}
void TreeNode::splitChild(int i, TreeNode *y) {
TreeNode *z = new TreeNode(y->t, y->leaf);
z->n = t - 1;
for (int j = 0; j < t - 1; j++)
z->keys[j] = y->keys[j + t];
if (y->leaf == false) {
for (int j = 0; j < t; j++)
z->C[j] = y->C[j + t];
}
y->n = t - 1;
for (int j = n; j >= i + 1; j--)
C[j + 1] = C[j];
C[i + 1] = z;
for (int j = n - 1; j >= i; j--)
keys[j + 1] = keys[j];
keys[i] = y->keys[t - 1];
n = n + 1;
}
int main() {
BTree t(3);
t.insert(8);
t.insert(9);
t.insert(10);
t.insert(11);
t.insert(15);
t.insert(16);
t.insert(17);
t.insert(18);
t.insert(20);
t.insert(23);
cout << "The B-tree is: ";
t.traverse();
int k = 10;
(t.search(k) != NULL) ? cout << endl
<< k << " is found"
: cout << endl
<< k << " is not Found";
k = 2;
(t.search(k) != NULL) ? cout << endl
<< k << " is found"
: cout << endl
<< k << " is not Found\n";
}
Searching Complexity on B Tree
Worst case Time complexity: Θ(log n)
Average case Time complexity: Θ(log n)
Best case Time complexity: Θ(log n)
Average case Space complexity: Θ(n)
Worst case Space complexity: Θ(n)
B Tree Applications
- databases and file systems
- to store blocks of data (secondary storage media)
- multilevel indexing