A B+ tree is an advanced form of a self-balancing tree in which all the values are present in the leaf level.
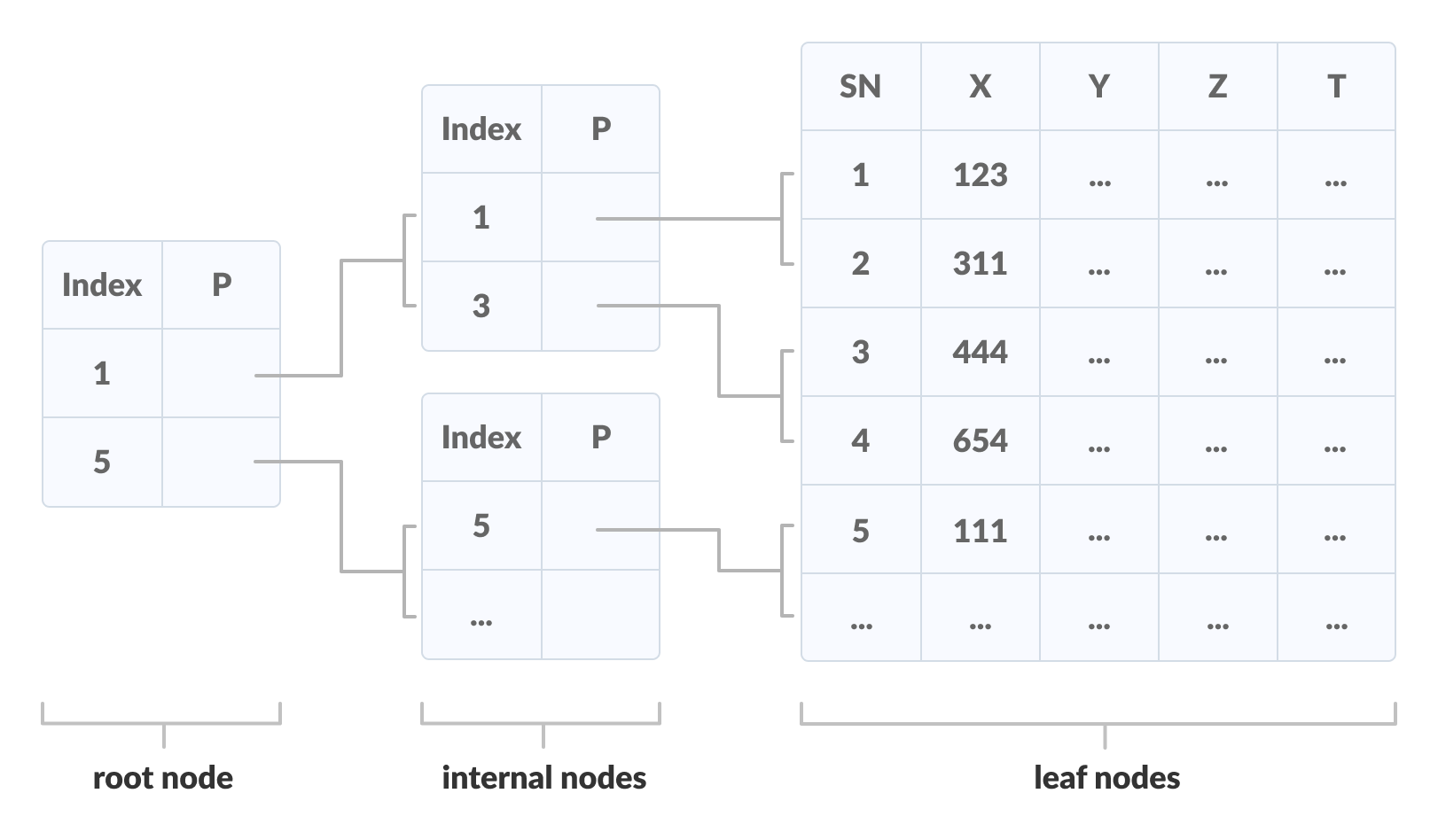
An important concept to be understood before learning B+ tree is multilevel indexing. In multilevel indexing, the index of indices is created as in figure below. It makes accessing the data easier and faster.
Properties of a B+ Tree
- All leaves are at the same level.
- The root has at least two children.
- Each node except root can have a maximum of m children and at least m/2 children.
- Each node can contain a maximum of m - 1 keys and a minimum of ⌈m/2⌉ - 1 keys.
Comparison between a B-tree and a B+ Tree
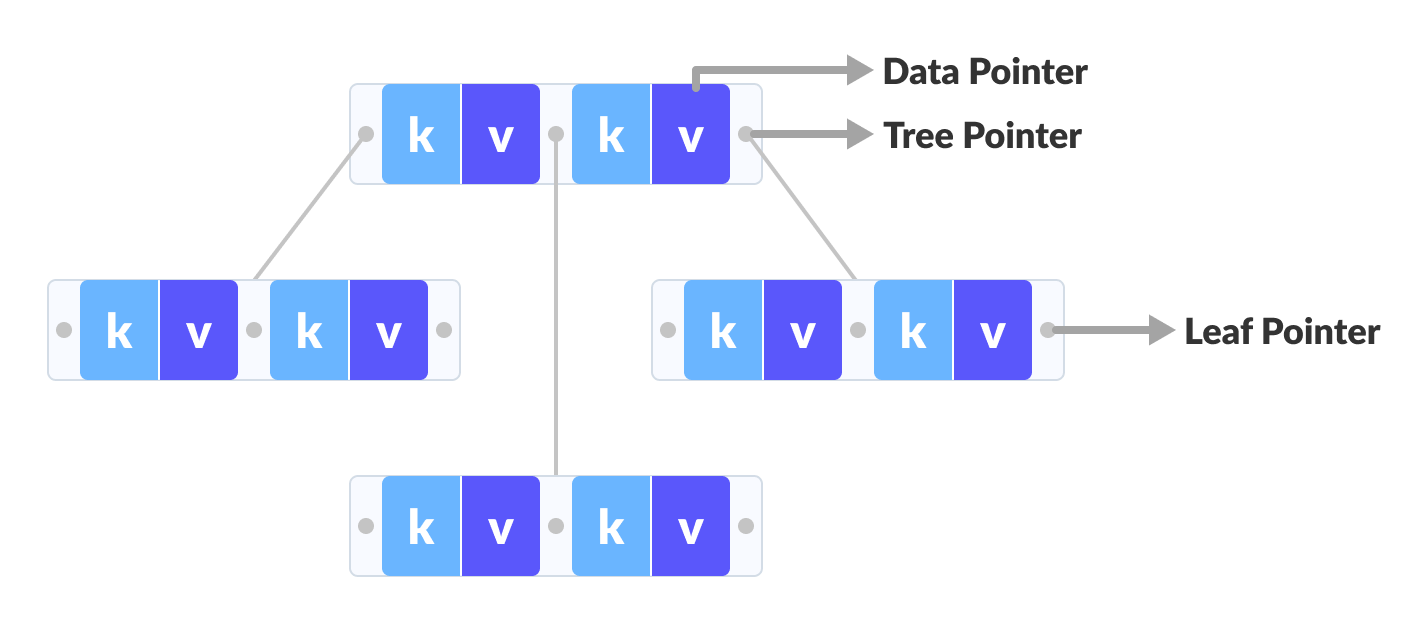
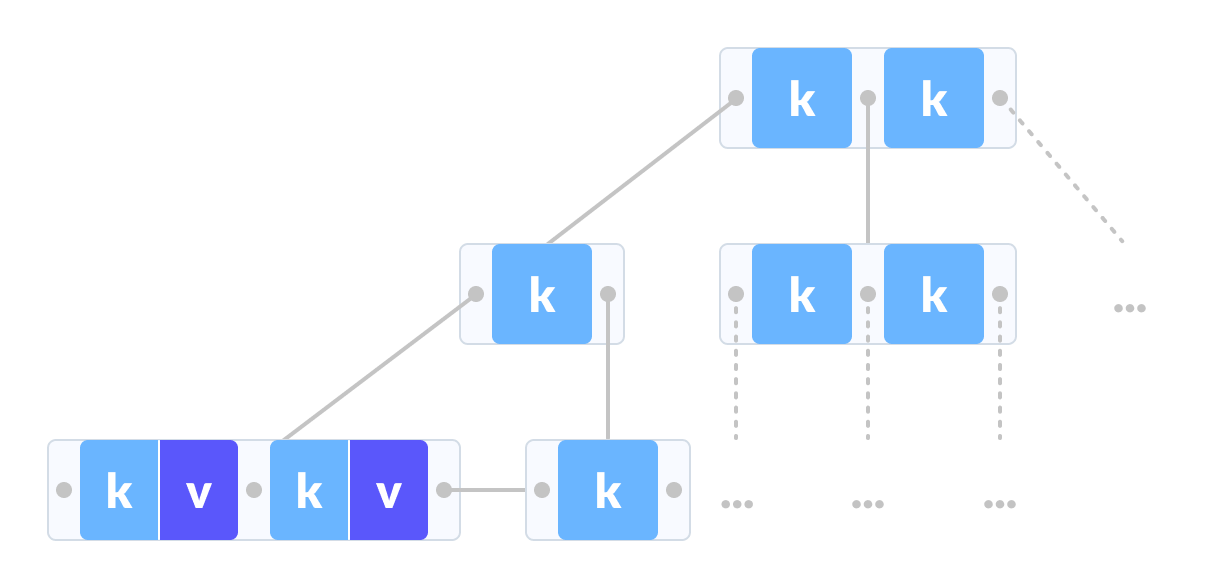
The data pointers are present only at the leaf nodes on a B+ tree whereas the data pointers are present in the internal, leaf or root nodes on a B-tree.
The leaves are not connected with each other on a B-tree whereas they are connected on a B+ tree.
Operations on a B+ tree are faster than on a B-tree.
Searching on a B+ Tree
The following steps are followed to search for data in a B+ Tree of order m. Let the data to be searched be k.
- Start from the root node. Compare k with the keys at the root node [k1, k2, k3,......km - 1.
- If k < k1, go to the left child of the root node.
- Else if k == k1, compare k2. If
k < k2, k lies between k1 and k2. So, search in the left child of k2. - If k > k2, go for k3, k4,...km-1 as in steps 2 and 3.
- Repeat the above steps until a leaf node is reached.
- If k exists in the leaf node, return true else return false.
Searching Example on a B+ Tree
Let us search k = 45 on the following B+ tree.
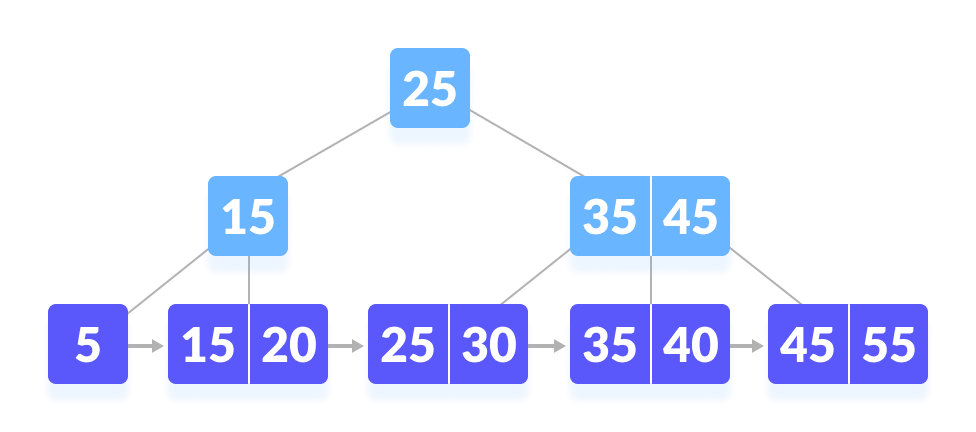
- Compare k with the root node.
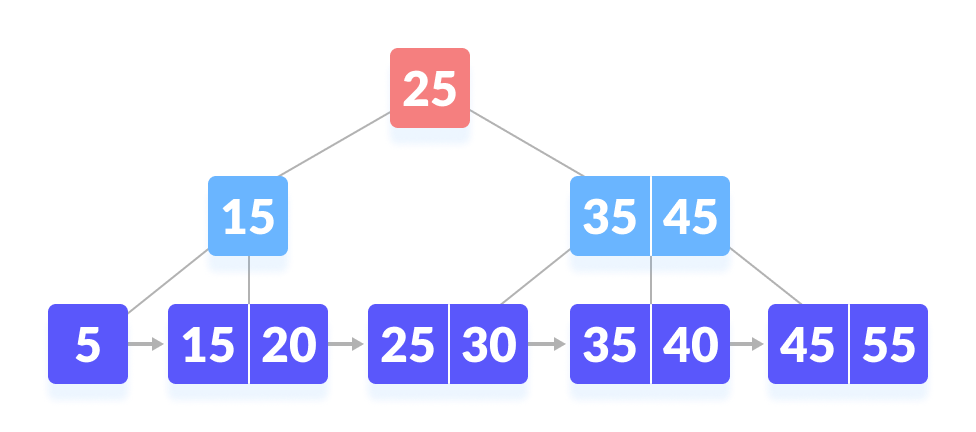
k is not found at the root - Since k > 25, go to the right child.
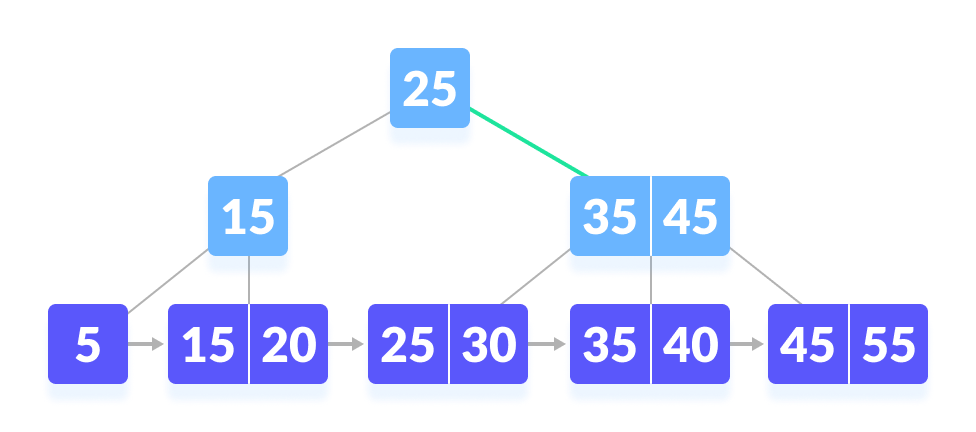
Go to right of the root - Compare k with 35. Since k > 30, compare k with 45.
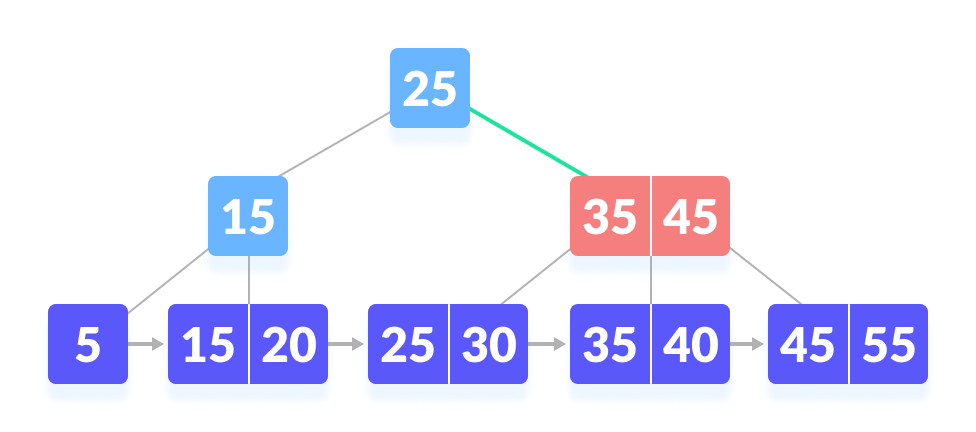
k not found - Since k ≥ 45, so go to the right child.
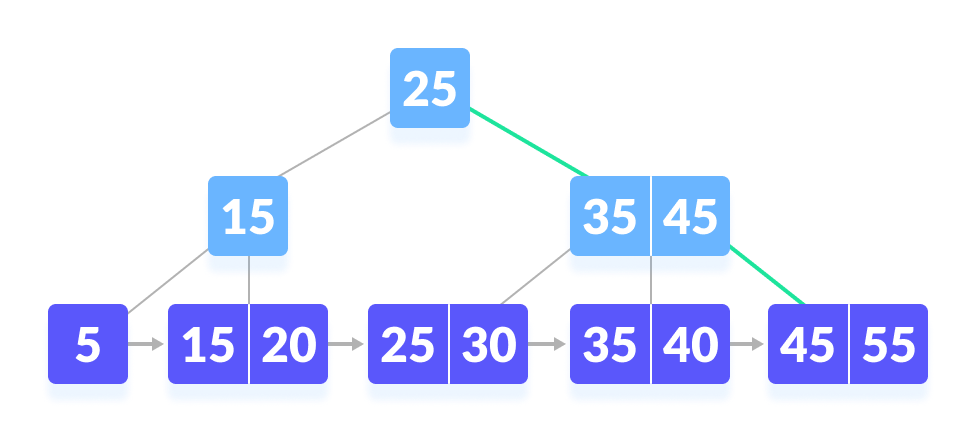
go to the right - k is found.
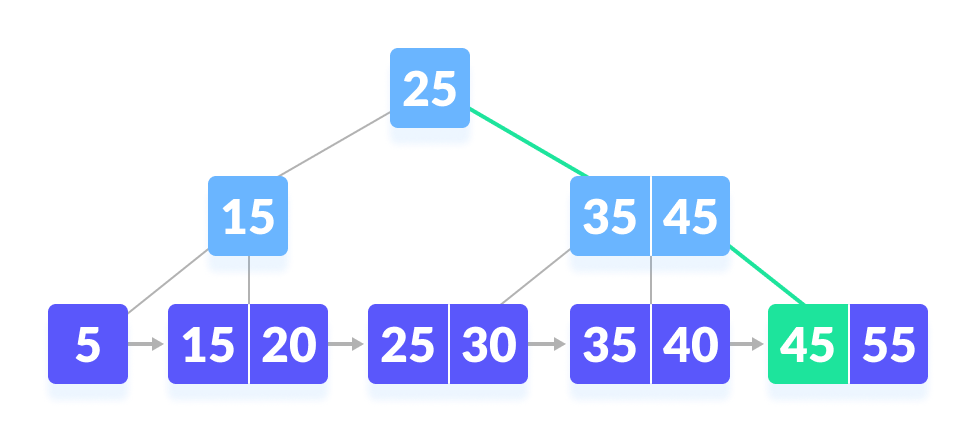
k is found
Python, Java and C/C++ Examples
# B+ tree in python
import math
# Node creation
class Node:
def __init__(self, order):
self.order = order
self.values = []
self.keys = []
self.nextKey = None
self.parent = None
self.check_leaf = False
# Insert at the leaf
def insert_at_leaf(self, leaf, value, key):
if (self.values):
temp1 = self.values
for i in range(len(temp1)):
if (value == temp1[i]):
self.keys[i].append(key)
break
elif (value < temp1[i]):
self.values = self.values[:i] + [value] + self.values[i:]
self.keys = self.keys[:i] + [[key]] + self.keys[i:]
break
elif (i + 1 == len(temp1)):
self.values.append(value)
self.keys.append([key])
break
else:
self.values = [value]
self.keys = [[key]]
# B plus tree
class BplusTree:
def __init__(self, order):
self.root = Node(order)
self.root.check_leaf = True
# Insert operation
def insert(self, value, key):
value = str(value)
old_node = self.search(value)
old_node.insert_at_leaf(old_node, value, key)
if (len(old_node.values) == old_node.order):
node1 = Node(old_node.order)
node1.check_leaf = True
node1.parent = old_node.parent
mid = int(math.ceil(old_node.order / 2)) - 1
node1.values = old_node.values[mid + 1:]
node1.keys = old_node.keys[mid + 1:]
node1.nextKey = old_node.nextKey
old_node.values = old_node.values[:mid + 1]
old_node.keys = old_node.keys[:mid + 1]
old_node.nextKey = node1
self.insert_in_parent(old_node, node1.values[0], node1)
# Search operation for different operations
def search(self, value):
current_node = self.root
while(current_node.check_leaf == False):
temp2 = current_node.values
for i in range(len(temp2)):
if (value == temp2[i]):
current_node = current_node.keys[i + 1]
break
elif (value < temp2[i]):
current_node = current_node.keys[i]
break
elif (i + 1 == len(current_node.values)):
current_node = current_node.keys[i + 1]
break
return current_node
# Find the node
def find(self, value, key):
l = self.search(value)
for i, item in enumerate(l.values):
if item == value:
if key in l.keys[i]:
return True
else:
return False
return False
# Inserting at the parent
def insert_in_parent(self, n, value, ndash):
if (self.root == n):
rootNode = Node(n.order)
rootNode.values = [value]
rootNode.keys = [n, ndash]
self.root = rootNode
n.parent = rootNode
ndash.parent = rootNode
return
parentNode = n.parent
temp3 = parentNode.keys
for i in range(len(temp3)):
if (temp3[i] == n):
parentNode.values = parentNode.values[:i] + \
[value] + parentNode.values[i:]
parentNode.keys = parentNode.keys[:i +
1] + [ndash] + parentNode.keys[i + 1:]
if (len(parentNode.keys) > parentNode.order):
parentdash = Node(parentNode.order)
parentdash.parent = parentNode.parent
mid = int(math.ceil(parentNode.order / 2)) - 1
parentdash.values = parentNode.values[mid + 1:]
parentdash.keys = parentNode.keys[mid + 1:]
value_ = parentNode.values[mid]
if (mid == 0):
parentNode.values = parentNode.values[:mid + 1]
else:
parentNode.values = parentNode.values[:mid]
parentNode.keys = parentNode.keys[:mid + 1]
for j in parentNode.keys:
j.parent = parentNode
for j in parentdash.keys:
j.parent = parentdash
self.insert_in_parent(parentNode, value_, parentdash)
# Delete a node
def delete(self, value, key):
node_ = self.search(value)
temp = 0
for i, item in enumerate(node_.values):
if item == value:
temp = 1
if key in node_.keys[i]:
if len(node_.keys[i]) > 1:
node_.keys[i].pop(node_.keys[i].index(key))
elif node_ == self.root:
node_.values.pop(i)
node_.keys.pop(i)
else:
node_.keys[i].pop(node_.keys[i].index(key))
del node_.keys[i]
node_.values.pop(node_.values.index(value))
self.deleteEntry(node_, value, key)
else:
print("Value not in Key")
return
if temp == 0:
print("Value not in Tree")
return
# Delete an entry
def deleteEntry(self, node_, value, key):
if not node_.check_leaf:
for i, item in enumerate(node_.keys):
if item == key:
node_.keys.pop(i)
break
for i, item in enumerate(node_.values):
if item == value:
node_.values.pop(i)
break
if self.root == node_ and len(node_.keys) == 1:
self.root = node_.keys[0]
node_.keys[0].parent = None
del node_
return
elif (len(node_.keys) < int(math.ceil(node_.order / 2)) and node_.check_leaf == False) or (len(node_.values) < int(math.ceil((node_.order - 1) / 2)) and node_.check_leaf == True):
is_predecessor = 0
parentNode = node_.parent
PrevNode = -1
NextNode = -1
PrevK = -1
PostK = -1
for i, item in enumerate(parentNode.keys):
if item == node_:
if i > 0:
PrevNode = parentNode.keys[i - 1]
PrevK = parentNode.values[i - 1]
if i < len(parentNode.keys) - 1:
NextNode = parentNode.keys[i + 1]
PostK = parentNode.values[i]
if PrevNode == -1:
ndash = NextNode
value_ = PostK
elif NextNode == -1:
is_predecessor = 1
ndash = PrevNode
value_ = PrevK
else:
if len(node_.values) + len(NextNode.values) < node_.order:
ndash = NextNode
value_ = PostK
else:
is_predecessor = 1
ndash = PrevNode
value_ = PrevK
if len(node_.values) + len(ndash.values) < node_.order:
if is_predecessor == 0:
node_, ndash = ndash, node_
ndash.keys += node_.keys
if not node_.check_leaf:
ndash.values.append(value_)
else:
ndash.nextKey = node_.nextKey
ndash.values += node_.values
if not ndash.check_leaf:
for j in ndash.keys:
j.parent = ndash
self.deleteEntry(node_.parent, value_, node_)
del node_
else:
if is_predecessor == 1:
if not node_.check_leaf:
ndashpm = ndash.keys.pop(-1)
ndashkm_1 = ndash.values.pop(-1)
node_.keys = [ndashpm] + node_.keys
node_.values = [value_] + node_.values
parentNode = node_.parent
for i, item in enumerate(parentNode.values):
if item == value_:
p.values[i] = ndashkm_1
break
else:
ndashpm = ndash.keys.pop(-1)
ndashkm = ndash.values.pop(-1)
node_.keys = [ndashpm] + node_.keys
node_.values = [ndashkm] + node_.values
parentNode = node_.parent
for i, item in enumerate(p.values):
if item == value_:
parentNode.values[i] = ndashkm
break
else:
if not node_.check_leaf:
ndashp0 = ndash.keys.pop(0)
ndashk0 = ndash.values.pop(0)
node_.keys = node_.keys + [ndashp0]
node_.values = node_.values + [value_]
parentNode = node_.parent
for i, item in enumerate(parentNode.values):
if item == value_:
parentNode.values[i] = ndashk0
break
else:
ndashp0 = ndash.keys.pop(0)
ndashk0 = ndash.values.pop(0)
node_.keys = node_.keys + [ndashp0]
node_.values = node_.values + [ndashk0]
parentNode = node_.parent
for i, item in enumerate(parentNode.values):
if item == value_:
parentNode.values[i] = ndash.values[0]
break
if not ndash.check_leaf:
for j in ndash.keys:
j.parent = ndash
if not node_.check_leaf:
for j in node_.keys:
j.parent = node_
if not parentNode.check_leaf:
for j in parentNode.keys:
j.parent = parentNode
# Print the tree
def printTree(tree):
lst = [tree.root]
level = [0]
leaf = None
flag = 0
lev_leaf = 0
node1 = Node(str(level[0]) + str(tree.root.values))
while (len(lst) != 0):
x = lst.pop(0)
lev = level.pop(0)
if (x.check_leaf == False):
for i, item in enumerate(x.keys):
print(item.values)
else:
for i, item in enumerate(x.keys):
print(item.values)
if (flag == 0):
lev_leaf = lev
leaf = x
flag = 1
record_len = 3
bplustree = BplusTree(record_len)
bplustree.insert('5', '33')
bplustree.insert('15', '21')
bplustree.insert('25', '31')
bplustree.insert('35', '41')
bplustree.insert('45', '10')
printTree(bplustree)
if(bplustree.find('5', '34')):
print("Found")
else:
print("Not found")
// Searching on a B+ tree in Java
import java.util.*;
public class BPlusTree {
int m;
InternalNode root;
LeafNode firstLeaf;
// Binary search program
private int binarySearch(DictionaryPair[] dps, int numPairs, int t) {
Comparator<DictionaryPair> c = new Comparator<DictionaryPair>() {
@Override
public int compare(DictionaryPair o1, DictionaryPair o2) {
Integer a = Integer.valueOf(o1.key);
Integer b = Integer.valueOf(o2.key);
return a.compareTo(b);
}
};
return Arrays.binarySearch(dps, 0, numPairs, new DictionaryPair(t, 0), c);
}
// Find the leaf node
private LeafNode findLeafNode(int key) {
Integer[] keys = this.root.keys;
int i;
for (i = 0; i < this.root.degree - 1; i++) {
if (key < keys[i]) {
break;
}
}
Node child = this.root.childPointers[i];
if (child instanceof LeafNode) {
return (LeafNode) child;
} else {
return findLeafNode((InternalNode) child, key);
}
}
// Find the leaf node
private LeafNode findLeafNode(InternalNode node, int key) {
Integer[] keys = node.keys;
int i;
for (i = 0; i < node.degree - 1; i++) {
if (key < keys[i]) {
break;
}
}
Node childNode = node.childPointers[i];
if (childNode instanceof LeafNode) {
return (LeafNode) childNode;
} else {
return findLeafNode((InternalNode) node.childPointers[i], key);
}
}
// Finding the index of the pointer
private int findIndexOfPointer(Node[] pointers, LeafNode node) {
int i;
for (i = 0; i < pointers.length; i++) {
if (pointers[i] == node) {
break;
}
}
return i;
}
// Get the mid point
private int getMidpoint() {
return (int) Math.ceil((this.m + 1) / 2.0) - 1;
}
// Balance the tree
private void handleDeficiency(InternalNode in) {
InternalNode sibling;
InternalNode parent = in.parent;
if (this.root == in) {
for (int i = 0; i < in.childPointers.length; i++) {
if (in.childPointers[i] != null) {
if (in.childPointers[i] instanceof InternalNode) {
this.root = (InternalNode) in.childPointers[i];
this.root.parent = null;
} else if (in.childPointers[i] instanceof LeafNode) {
this.root = null;
}
}
}
}
else if (in.leftSibling != null && in.leftSibling.isLendable()) {
sibling = in.leftSibling;
} else if (in.rightSibling != null && in.rightSibling.isLendable()) {
sibling = in.rightSibling;
int borrowedKey = sibling.keys[0];
Node pointer = sibling.childPointers[0];
in.keys[in.degree - 1] = parent.keys[0];
in.childPointers[in.degree] = pointer;
parent.keys[0] = borrowedKey;
sibling.removePointer(0);
Arrays.sort(sibling.keys);
sibling.removePointer(0);
shiftDown(in.childPointers, 1);
} else if (in.leftSibling != null && in.leftSibling.isMergeable()) {
} else if (in.rightSibling != null && in.rightSibling.isMergeable()) {
sibling = in.rightSibling;
sibling.keys[sibling.degree - 1] = parent.keys[parent.degree - 2];
Arrays.sort(sibling.keys, 0, sibling.degree);
parent.keys[parent.degree - 2] = null;
for (int i = 0; i < in.childPointers.length; i++) {
if (in.childPointers[i] != null) {
sibling.prependChildPointer(in.childPointers[i]);
in.childPointers[i].parent = sibling;
in.removePointer(i);
}
}
parent.removePointer(in);
sibling.leftSibling = in.leftSibling;
}
if (parent != null && parent.isDeficient()) {
handleDeficiency(parent);
}
}
private boolean isEmpty() {
return firstLeaf == null;
}
private int linearNullSearch(DictionaryPair[] dps) {
for (int i = 0; i < dps.length; i++) {
if (dps[i] == null) {
return i;
}
}
return -1;
}
private int linearNullSearch(Node[] pointers) {
for (int i = 0; i < pointers.length; i++) {
if (pointers[i] == null) {
return i;
}
}
return -1;
}
private void shiftDown(Node[] pointers, int amount) {
Node[] newPointers = new Node[this.m + 1];
for (int i = amount; i < pointers.length; i++) {
newPointers[i - amount] = pointers[i];
}
pointers = newPointers;
}
private void sortDictionary(DictionaryPair[] dictionary) {
Arrays.sort(dictionary, new Comparator<DictionaryPair>() {
@Override
public int compare(DictionaryPair o1, DictionaryPair o2) {
if (o1 == null && o2 == null) {
return 0;
}
if (o1 == null) {
return 1;
}
if (o2 == null) {
return -1;
}
return o1.compareTo(o2);
}
});
}
private Node[] splitChildPointers(InternalNode in, int split) {
Node[] pointers = in.childPointers;
Node[] halfPointers = new Node[this.m + 1];
for (int i = split + 1; i < pointers.length; i++) {
halfPointers[i - split - 1] = pointers[i];
in.removePointer(i);
}
return halfPointers;
}
private DictionaryPair[] splitDictionary(LeafNode ln, int split) {
DictionaryPair[] dictionary = ln.dictionary;
DictionaryPair[] halfDict = new DictionaryPair[this.m];
for (int i = split; i < dictionary.length; i++) {
halfDict[i - split] = dictionary[i];
ln.delete(i);
}
return halfDict;
}
private void splitInternalNode(InternalNode in) {
InternalNode parent = in.parent;
int midpoint = getMidpoint();
int newParentKey = in.keys[midpoint];
Integer[] halfKeys = splitKeys(in.keys, midpoint);
Node[] halfPointers = splitChildPointers(in, midpoint);
in.degree = linearNullSearch(in.childPointers);
InternalNode sibling = new InternalNode(this.m, halfKeys, halfPointers);
for (Node pointer : halfPointers) {
if (pointer != null) {
pointer.parent = sibling;
}
}
sibling.rightSibling = in.rightSibling;
if (sibling.rightSibling != null) {
sibling.rightSibling.leftSibling = sibling;
}
in.rightSibling = sibling;
sibling.leftSibling = in;
if (parent == null) {
Integer[] keys = new Integer[this.m];
keys[0] = newParentKey;
InternalNode newRoot = new InternalNode(this.m, keys);
newRoot.appendChildPointer(in);
newRoot.appendChildPointer(sibling);
this.root = newRoot;
in.parent = newRoot;
sibling.parent = newRoot;
} else {
parent.keys[parent.degree - 1] = newParentKey;
Arrays.sort(parent.keys, 0, parent.degree);
int pointerIndex = parent.findIndexOfPointer(in) + 1;
parent.insertChildPointer(sibling, pointerIndex);
sibling.parent = parent;
}
}
private Integer[] splitKeys(Integer[] keys, int split) {
Integer[] halfKeys = new Integer[this.m];
keys[split] = null;
for (int i = split + 1; i < keys.length; i++) {
halfKeys[i - split - 1] = keys[i];
keys[i] = null;
}
return halfKeys;
}
public void insert(int key, double value) {
if (isEmpty()) {
LeafNode ln = new LeafNode(this.m, new DictionaryPair(key, value));
this.firstLeaf = ln;
} else {
LeafNode ln = (this.root == null) ? this.firstLeaf : findLeafNode(key);
if (!ln.insert(new DictionaryPair(key, value))) {
ln.dictionary[ln.numPairs] = new DictionaryPair(key, value);
ln.numPairs++;
sortDictionary(ln.dictionary);
int midpoint = getMidpoint();
DictionaryPair[] halfDict = splitDictionary(ln, midpoint);
if (ln.parent == null) {
Integer[] parent_keys = new Integer[this.m];
parent_keys[0] = halfDict[0].key;
InternalNode parent = new InternalNode(this.m, parent_keys);
ln.parent = parent;
parent.appendChildPointer(ln);
} else {
int newParentKey = halfDict[0].key;
ln.parent.keys[ln.parent.degree - 1] = newParentKey;
Arrays.sort(ln.parent.keys, 0, ln.parent.degree);
}
LeafNode newLeafNode = new LeafNode(this.m, halfDict, ln.parent);
int pointerIndex = ln.parent.findIndexOfPointer(ln) + 1;
ln.parent.insertChildPointer(newLeafNode, pointerIndex);
newLeafNode.rightSibling = ln.rightSibling;
if (newLeafNode.rightSibling != null) {
newLeafNode.rightSibling.leftSibling = newLeafNode;
}
ln.rightSibling = newLeafNode;
newLeafNode.leftSibling = ln;
if (this.root == null) {
this.root = ln.parent;
} else {
InternalNode in = ln.parent;
while (in != null) {
if (in.isOverfull()) {
splitInternalNode(in);
} else {
break;
}
in = in.parent;
}
}
}
}
}
public Double search(int key) {
if (isEmpty()) {
return null;
}
LeafNode ln = (this.root == null) ? this.firstLeaf : findLeafNode(key);
DictionaryPair[] dps = ln.dictionary;
int index = binarySearch(dps, ln.numPairs, key);
if (index < 0) {
return null;
} else {
return dps[index].value;
}
}
public ArrayList<Double> search(int lowerBound, int upperBound) {
ArrayList<Double> values = new ArrayList<Double>();
LeafNode currNode = this.firstLeaf;
while (currNode != null) {
DictionaryPair dps[] = currNode.dictionary;
for (DictionaryPair dp : dps) {
if (dp == null) {
break;
}
if (lowerBound <= dp.key && dp.key <= upperBound) {
values.add(dp.value);
}
}
currNode = currNode.rightSibling;
}
return values;
}
public BPlusTree(int m) {
this.m = m;
this.root = null;
}
public class Node {
InternalNode parent;
}
private class InternalNode extends Node {
int maxDegree;
int minDegree;
int degree;
InternalNode leftSibling;
InternalNode rightSibling;
Integer[] keys;
Node[] childPointers;
private void appendChildPointer(Node pointer) {
this.childPointers[degree] = pointer;
this.degree++;
}
private int findIndexOfPointer(Node pointer) {
for (int i = 0; i < childPointers.length; i++) {
if (childPointers[i] == pointer) {
return i;
}
}
return -1;
}
private void insertChildPointer(Node pointer, int index) {
for (int i = degree - 1; i >= index; i--) {
childPointers[i + 1] = childPointers[i];
}
this.childPointers[index] = pointer;
this.degree++;
}
private boolean isDeficient() {
return this.degree < this.minDegree;
}
private boolean isLendable() {
return this.degree > this.minDegree;
}
private boolean isMergeable() {
return this.degree == this.minDegree;
}
private boolean isOverfull() {
return this.degree == maxDegree + 1;
}
private void prependChildPointer(Node pointer) {
for (int i = degree - 1; i >= 0; i--) {
childPointers[i + 1] = childPointers[i];
}
this.childPointers[0] = pointer;
this.degree++;
}
private void removeKey(int index) {
this.keys[index] = null;
}
private void removePointer(int index) {
this.childPointers[index] = null;
this.degree--;
}
private void removePointer(Node pointer) {
for (int i = 0; i < childPointers.length; i++) {
if (childPointers[i] == pointer) {
this.childPointers[i] = null;
}
}
this.degree--;
}
private InternalNode(int m, Integer[] keys) {
this.maxDegree = m;
this.minDegree = (int) Math.ceil(m / 2.0);
this.degree = 0;
this.keys = keys;
this.childPointers = new Node[this.maxDegree + 1];
}
private InternalNode(int m, Integer[] keys, Node[] pointers) {
this.maxDegree = m;
this.minDegree = (int) Math.ceil(m / 2.0);
this.degree = linearNullSearch(pointers);
this.keys = keys;
this.childPointers = pointers;
}
}
public class LeafNode extends Node {
int maxNumPairs;
int minNumPairs;
int numPairs;
LeafNode leftSibling;
LeafNode rightSibling;
DictionaryPair[] dictionary;
public void delete(int index) {
this.dictionary[index] = null;
numPairs--;
}
public boolean insert(DictionaryPair dp) {
if (this.isFull()) {
return false;
} else {
this.dictionary[numPairs] = dp;
numPairs++;
Arrays.sort(this.dictionary, 0, numPairs);
return true;
}
}
public boolean isDeficient() {
return numPairs < minNumPairs;
}
public boolean isFull() {
return numPairs == maxNumPairs;
}
public boolean isLendable() {
return numPairs > minNumPairs;
}
public boolean isMergeable() {
return numPairs == minNumPairs;
}
public LeafNode(int m, DictionaryPair dp) {
this.maxNumPairs = m - 1;
this.minNumPairs = (int) (Math.ceil(m / 2) - 1);
this.dictionary = new DictionaryPair[m];
this.numPairs = 0;
this.insert(dp);
}
public LeafNode(int m, DictionaryPair[] dps, InternalNode parent) {
this.maxNumPairs = m - 1;
this.minNumPairs = (int) (Math.ceil(m / 2) - 1);
this.dictionary = dps;
this.numPairs = linearNullSearch(dps);
this.parent = parent;
}
}
public class DictionaryPair implements Comparable<DictionaryPair> {
int key;
double value;
public DictionaryPair(int key, double value) {
this.key = key;
this.value = value;
}
public int compareTo(DictionaryPair o) {
if (key == o.key) {
return 0;
} else if (key > o.key) {
return 1;
} else {
return -1;
}
}
}
public static void main(String[] args) {
BPlusTree bpt = null;
bpt = new BPlusTree(3);
bpt.insert(5, 33);
bpt.insert(15, 21);
bpt.insert(25, 31);
bpt.insert(35, 41);
bpt.insert(45, 10);
if (bpt.search(15) != null) {
System.out.println("Found");
} else {
System.out.println("Not Found");
}
;
}
}
// Searching on a B+ Tree in C
#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// Default order
#define ORDER 3
typedef struct record {
int value;
} record;
// Node
typedef struct node {
void **pointers;
int *keys;
struct node *parent;
bool is_leaf;
int num_keys;
struct node *next;
} node;
int order = ORDER;
node *queue = NULL;
bool verbose_output = false;
// Enqueue
void enqueue(node *new_node);
// Dequeue
node *dequeue(void);
int height(node *const root);
int pathToLeaves(node *const root, node *child);
void printLeaves(node *const root);
void printTree(node *const root);
void findAndPrint(node *const root, int key, bool verbose);
void findAndPrintRange(node *const root, int range1, int range2, bool verbose);
int findRange(node *const root, int key_start, int key_end, bool verbose,
int returned_keys[], void *returned_pointers[]);
node *findLeaf(node *const root, int key, bool verbose);
record *find(node *root, int key, bool verbose, node **leaf_out);
int cut(int length);
record *makeRecord(int value);
node *makeNode(void);
node *makeLeaf(void);
int getLeftIndex(node *parent, node *left);
node *insertIntoLeaf(node *leaf, int key, record *pointer);
node *insertIntoLeafAfterSplitting(node *root, node *leaf, int key,
record *pointer);
node *insertIntoNode(node *root, node *parent,
int left_index, int key, node *right);
node *insertIntoNodeAfterSplitting(node *root, node *parent,
int left_index,
int key, node *right);
node *insertIntoParent(node *root, node *left, int key, node *right);
node *insertIntoNewRoot(node *left, int key, node *right);
node *startNewTree(int key, record *pointer);
node *insert(node *root, int key, int value);
// Enqueue
void enqueue(node *new_node) {
node *c;
if (queue == NULL) {
queue = new_node;
queue->next = NULL;
} else {
c = queue;
while (c->next != NULL) {
c = c->next;
}
c->next = new_node;
new_node->next = NULL;
}
}
// Dequeue
node *dequeue(void) {
node *n = queue;
queue = queue->next;
n->next = NULL;
return n;
}
// Print the leaves
void printLeaves(node *const root) {
if (root == NULL) {
printf("Empty tree.\n");
return;
}
int i;
node *c = root;
while (!c->is_leaf)
c = c->pointers[0];
while (true) {
for (i = 0; i < c->num_keys; i++) {
if (verbose_output)
printf("%p ", c->pointers[i]);
printf("%d ", c->keys[i]);
}
if (verbose_output)
printf("%p ", c->pointers[order - 1]);
if (c->pointers[order - 1] != NULL) {
printf(" | ");
c = c->pointers[order - 1];
} else
break;
}
printf("\n");
}
// Calculate height
int height(node *const root) {
int h = 0;
node *c = root;
while (!c->is_leaf) {
c = c->pointers[0];
h++;
}
return h;
}
// Get path to root
int pathToLeaves(node *const root, node *child) {
int length = 0;
node *c = child;
while (c != root) {
c = c->parent;
length++;
}
return length;
}
// Print the tree
void printTree(node *const root) {
node *n = NULL;
int i = 0;
int rank = 0;
int new_rank = 0;
if (root == NULL) {
printf("Empty tree.\n");
return;
}
queue = NULL;
enqueue(root);
while (queue != NULL) {
n = dequeue();
if (n->parent != NULL && n == n->parent->pointers[0]) {
new_rank = pathToLeaves(root, n);
if (new_rank != rank) {
rank = new_rank;
printf("\n");
}
}
if (verbose_output)
printf("(%p)", n);
for (i = 0; i < n->num_keys; i++) {
if (verbose_output)
printf("%p ", n->pointers[i]);
printf("%d ", n->keys[i]);
}
if (!n->is_leaf)
for (i = 0; i <= n->num_keys; i++)
enqueue(n->pointers[i]);
if (verbose_output) {
if (n->is_leaf)
printf("%p ", n->pointers[order - 1]);
else
printf("%p ", n->pointers[n->num_keys]);
}
printf("| ");
}
printf("\n");
}
// Find the node and print it
void findAndPrint(node *const root, int key, bool verbose) {
node *leaf = NULL;
record *r = find(root, key, verbose, NULL);
if (r == NULL)
printf("Record not found under key %d.\n", key);
else
printf("Record at %p -- key %d, value %d.\n",
r, key, r->value);
}
// Find and print the range
void findAndPrintRange(node *const root, int key_start, int key_end,
bool verbose) {
int i;
int array_size = key_end - key_start + 1;
int returned_keys[array_size];
void *returned_pointers[array_size];
int num_found = findRange(root, key_start, key_end, verbose,
returned_keys, returned_pointers);
if (!num_found)
printf("None found.\n");
else {
for (i = 0; i < num_found; i++)
printf("Key: %d Location: %p Value: %d\n",
returned_keys[i],
returned_pointers[i],
((record *)
returned_pointers[i])
->value);
}
}
// Find the range
int findRange(node *const root, int key_start, int key_end, bool verbose,
int returned_keys[], void *returned_pointers[]) {
int i, num_found;
num_found = 0;
node *n = findLeaf(root, key_start, verbose);
if (n == NULL)
return 0;
for (i = 0; i < n->num_keys && n->keys[i] < key_start; i++)
;
if (i == n->num_keys)
return 0;
while (n != NULL) {
for (; i < n->num_keys && n->keys[i] <= key_end; i++) {
returned_keys[num_found] = n->keys[i];
returned_pointers[num_found] = n->pointers[i];
num_found++;
}
n = n->pointers[order - 1];
i = 0;
}
return num_found;
}
// Find the leaf
node *findLeaf(node *const root, int key, bool verbose) {
if (root == NULL) {
if (verbose)
printf("Empty tree.\n");
return root;
}
int i = 0;
node *c = root;
while (!c->is_leaf) {
if (verbose) {
printf("[");
for (i = 0; i < c->num_keys - 1; i++)
printf("%d ", c->keys[i]);
printf("%d] ", c->keys[i]);
}
i = 0;
while (i < c->num_keys) {
if (key >= c->keys[i])
i++;
else
break;
}
if (verbose)
printf("%d ->\n", i);
c = (node *)c->pointers[i];
}
if (verbose) {
printf("Leaf [");
for (i = 0; i < c->num_keys - 1; i++)
printf("%d ", c->keys[i]);
printf("%d] ->\n", c->keys[i]);
}
return c;
}
record *find(node *root, int key, bool verbose, node **leaf_out) {
if (root == NULL) {
if (leaf_out != NULL) {
*leaf_out = NULL;
}
return NULL;
}
int i = 0;
node *leaf = NULL;
leaf = findLeaf(root, key, verbose);
for (i = 0; i < leaf->num_keys; i++)
if (leaf->keys[i] == key)
break;
if (leaf_out != NULL) {
*leaf_out = leaf;
}
if (i == leaf->num_keys)
return NULL;
else
return (record *)leaf->pointers[i];
}
int cut(int length) {
if (length % 2 == 0)
return length / 2;
else
return length / 2 + 1;
}
record *makeRecord(int value) {
record *new_record = (record *)malloc(sizeof(record));
if (new_record == NULL) {
perror("Record creation.");
exit(EXIT_FAILURE);
} else {
new_record->value = value;
}
return new_record;
}
node *makeNode(void) {
node *new_node;
new_node = malloc(sizeof(node));
if (new_node == NULL) {
perror("Node creation.");
exit(EXIT_FAILURE);
}
new_node->keys = malloc((order - 1) * sizeof(int));
if (new_node->keys == NULL) {
perror("New node keys array.");
exit(EXIT_FAILURE);
}
new_node->pointers = malloc(order * sizeof(void *));
if (new_node->pointers == NULL) {
perror("New node pointers array.");
exit(EXIT_FAILURE);
}
new_node->is_leaf = false;
new_node->num_keys = 0;
new_node->parent = NULL;
new_node->next = NULL;
return new_node;
}
node *makeLeaf(void) {
node *leaf = makeNode();
leaf->is_leaf = true;
return leaf;
}
int getLeftIndex(node *parent, node *left) {
int left_index = 0;
while (left_index <= parent->num_keys &&
parent->pointers[left_index] != left)
left_index++;
return left_index;
}
node *insertIntoLeaf(node *leaf, int key, record *pointer) {
int i, insertion_point;
insertion_point = 0;
while (insertion_point < leaf->num_keys && leaf->keys[insertion_point] < key)
insertion_point++;
for (i = leaf->num_keys; i > insertion_point; i--) {
leaf->keys[i] = leaf->keys[i - 1];
leaf->pointers[i] = leaf->pointers[i - 1];
}
leaf->keys[insertion_point] = key;
leaf->pointers[insertion_point] = pointer;
leaf->num_keys++;
return leaf;
}
node *insertIntoLeafAfterSplitting(node *root, node *leaf, int key, record *pointer) {
node *new_leaf;
int *temp_keys;
void **temp_pointers;
int insertion_index, split, new_key, i, j;
new_leaf = makeLeaf();
temp_keys = malloc(order * sizeof(int));
if (temp_keys == NULL) {
perror("Temporary keys array.");
exit(EXIT_FAILURE);
}
temp_pointers = malloc(order * sizeof(void *));
if (temp_pointers == NULL) {
perror("Temporary pointers array.");
exit(EXIT_FAILURE);
}
insertion_index = 0;
while (insertion_index < order - 1 && leaf->keys[insertion_index] < key)
insertion_index++;
for (i = 0, j = 0; i < leaf->num_keys; i++, j++) {
if (j == insertion_index)
j++;
temp_keys[j] = leaf->keys[i];
temp_pointers[j] = leaf->pointers[i];
}
temp_keys[insertion_index] = key;
temp_pointers[insertion_index] = pointer;
leaf->num_keys = 0;
split = cut(order - 1);
for (i = 0; i < split; i++) {
leaf->pointers[i] = temp_pointers[i];
leaf->keys[i] = temp_keys[i];
leaf->num_keys++;
}
for (i = split, j = 0; i < order; i++, j++) {
new_leaf->pointers[j] = temp_pointers[i];
new_leaf->keys[j] = temp_keys[i];
new_leaf->num_keys++;
}
free(temp_pointers);
free(temp_keys);
new_leaf->pointers[order - 1] = leaf->pointers[order - 1];
leaf->pointers[order - 1] = new_leaf;
for (i = leaf->num_keys; i < order - 1; i++)
leaf->pointers[i] = NULL;
for (i = new_leaf->num_keys; i < order - 1; i++)
new_leaf->pointers[i] = NULL;
new_leaf->parent = leaf->parent;
new_key = new_leaf->keys[0];
return insertIntoParent(root, leaf, new_key, new_leaf);
}
node *insertIntoNode(node *root, node *n,
int left_index, int key, node *right) {
int i;
for (i = n->num_keys; i > left_index; i--) {
n->pointers[i + 1] = n->pointers[i];
n->keys[i] = n->keys[i - 1];
}
n->pointers[left_index + 1] = right;
n->keys[left_index] = key;
n->num_keys++;
return root;
}
node *insertIntoNodeAfterSplitting(node *root, node *old_node, int left_index,
int key, node *right) {
int i, j, split, k_prime;
node *new_node, *child;
int *temp_keys;
node **temp_pointers;
temp_pointers = malloc((order + 1) * sizeof(node *));
if (temp_pointers == NULL) {
exit(EXIT_FAILURE);
}
temp_keys = malloc(order * sizeof(int));
if (temp_keys == NULL) {
exit(EXIT_FAILURE);
}
for (i = 0, j = 0; i < old_node->num_keys + 1; i++, j++) {
if (j == left_index + 1)
j++;
temp_pointers[j] = old_node->pointers[i];
}
for (i = 0, j = 0; i < old_node->num_keys; i++, j++) {
if (j == left_index)
j++;
temp_keys[j] = old_node->keys[i];
}
temp_pointers[left_index + 1] = right;
temp_keys[left_index] = key;
split = cut(order);
new_node = makeNode();
old_node->num_keys = 0;
for (i = 0; i < split - 1; i++) {
old_node->pointers[i] = temp_pointers[i];
old_node->keys[i] = temp_keys[i];
old_node->num_keys++;
}
old_node->pointers[i] = temp_pointers[i];
k_prime = temp_keys[split - 1];
for (++i, j = 0; i < order; i++, j++) {
new_node->pointers[j] = temp_pointers[i];
new_node->keys[j] = temp_keys[i];
new_node->num_keys++;
}
new_node->pointers[j] = temp_pointers[i];
free(temp_pointers);
free(temp_keys);
new_node->parent = old_node->parent;
for (i = 0; i <= new_node->num_keys; i++) {
child = new_node->pointers[i];
child->parent = new_node;
}
return insertIntoParent(root, old_node, k_prime, new_node);
}
node *insertIntoParent(node *root, node *left, int key, node *right) {
int left_index;
node *parent;
parent = left->parent;
if (parent == NULL)
return insertIntoNewRoot(left, key, right);
left_index = getLeftIndex(parent, left);
if (parent->num_keys < order - 1)
return insertIntoNode(root, parent, left_index, key, right);
return insertIntoNodeAfterSplitting(root, parent, left_index, key, right);
}
node *insertIntoNewRoot(node *left, int key, node *right) {
node *root = makeNode();
root->keys[0] = key;
root->pointers[0] = left;
root->pointers[1] = right;
root->num_keys++;
root->parent = NULL;
left->parent = root;
right->parent = root;
return root;
}
node *startNewTree(int key, record *pointer) {
node *root = makeLeaf();
root->keys[0] = key;
root->pointers[0] = pointer;
root->pointers[order - 1] = NULL;
root->parent = NULL;
root->num_keys++;
return root;
}
node *insert(node *root, int key, int value) {
record *record_pointer = NULL;
node *leaf = NULL;
record_pointer = find(root, key, false, NULL);
if (record_pointer != NULL) {
record_pointer->value = value;
return root;
}
record_pointer = makeRecord(value);
if (root == NULL)
return startNewTree(key, record_pointer);
leaf = findLeaf(root, key, false);
if (leaf->num_keys < order - 1) {
leaf = insertIntoLeaf(leaf, key, record_pointer);
return root;
}
return insertIntoLeafAfterSplitting(root, leaf, key, record_pointer);
}
int main() {
node *root;
char instruction;
root = NULL;
root = insert(root, 5, 33);
root = insert(root, 15, 21);
root = insert(root, 25, 31);
root = insert(root, 35, 41);
root = insert(root, 45, 10);
printTree(root);
findAndPrint(root, 15, instruction = 'a');
}
// Searching on a B+ tree in C++
#include <iostream>
#include <vector>
#include <cmath>
#include <string>
using namespace std;
// node creation
class Node {
public:
int order;
vector<string> values;
vector<Node*> children; // for internal nodes
vector<vector<string>> keys; // for leaf nodes
Node* nextKey;
Node* parent;
bool check_leaf;
Node(int order) {
this->order = order;
this->nextKey = nullptr;
this->parent = nullptr;
this->check_leaf = false;
}
// insert at the leaf
void insert_at_leaf(Node* leaf, string value, string key) {
if (!values.empty()) {
for (int i = 0; i < values.size(); i++) {
if (value == values[i]) {
keys[i].push_back(key);
break;
}
else if (value < values[i]) {
values.insert(values.begin() + i, value);
keys.insert(keys.begin() + i, vector<string>{key});
break;
}
else if (i + 1 == values.size()) {
values.push_back(value);
keys.push_back(vector<string>{key});
break;
}
}
}
else {
values.push_back(value);
keys.push_back(vector<string>{key});
}
}
};
// B+ tree
class BplusTree {
public:
Node* root;
BplusTree(int order) {
root = new Node(order);
root->check_leaf = true;
}
// insert operation
void insert(string value, string key) {
Node* old_node = search(value);
old_node->insert_at_leaf(old_node, value, key);
if (old_node->values.size() == old_node->order) {
Node* node1 = new Node(old_node->order);
node1->check_leaf = true;
node1->parent = old_node->parent;
int mid = ceil(old_node->order / 2.0) - 1;
node1->values.assign(old_node->values.begin() + mid + 1, old_node->values.end());
node1->keys.assign(old_node->keys.begin() + mid + 1, old_node->keys.end());
node1->nextKey = old_node->nextKey;
old_node->values.resize(mid + 1);
old_node->keys.resize(mid + 1);
old_node->nextKey = node1;
insert_in_parent(old_node, node1->values[0], node1);
}
}
// search operation for different operations
Node* search(string value) {
Node* current_node = root;
while (!current_node->check_leaf) {
for (int i = 0; i < current_node->values.size(); i++) {
if (value == current_node->values[i]) {
current_node = current_node->children[i + 1];
break;
}
else if (value < current_node->values[i]) {
current_node = current_node->children[i];
break;
}
else if (i + 1 == current_node->values.size()) {
current_node = current_node->children[i + 1];
break;
}
}
}
return current_node;
}
// find the node
bool find(string value, string key) {
Node* l = search(value);
for (int i = 0; i < l->values.size(); i++) {
if (l->values[i] == value) {
for (int j = 0; j < l->keys[i].size(); j++) {
if (l->keys[i][j] == key) {
return true;
}
}
}
}
return false;
}
// inserting at the parent
void insert_in_parent(Node* n, string value, Node* ndash) {
if (root == n) {
Node* rootNode = new Node(n->order);
rootNode->values.push_back(value);
rootNode->children.push_back(n);
rootNode->children.push_back(ndash);
root = rootNode;
n->parent = rootNode;
ndash->parent = rootNode;
return;
}
Node* parentNode = n->parent;
for (int i = 0; i < parentNode->children.size(); i++) {
if (parentNode->children[i] == n) {
parentNode->values.insert(parentNode->values.begin() + i, value);
parentNode->children.insert(parentNode->children.begin() + i + 1, ndash);
if (parentNode->children.size() > parentNode->order) {
Node* parentdash = new Node(parentNode->order);
parentdash->parent = parentNode->parent;
int mid = ceil(parentNode->order / 2.0) - 1;
parentdash->values.assign(parentNode->values.begin() + mid + 1, parentNode->values.end());
parentdash->children.assign(parentNode->children.begin() + mid + 1, parentNode->children.end());
string value_ = parentNode->values[mid];
parentNode->values.resize(mid);
parentNode->children.resize(mid + 1);
insert_in_parent(parentNode, value_, parentdash);
}
break;
}
}
}
// display the tree
void printTree(Node* node) {
if (node == nullptr) return;
for (int i = 0; i < node->values.size(); i++) {
cout << node->values[i] << " ";
}
cout << endl;
if (!node->check_leaf) {
for (int i = 0; i <= node->values.size(); i++) {
printTree(node->children[i]);
}
}
}
};
int main() {
int record_len = 3;
BplusTree bplustree(record_len);
bplustree.insert("5", "33");
bplustree.insert("15", "21");
bplustree.insert("25", "31");
bplustree.insert("35", "41");
bplustree.insert("45", "10");
bplustree.printTree(bplustree.root);
if (bplustree.find("5", "34")) {
cout << "Found" << endl;
} else {
cout << "Not found" << endl;
}
return 0;
}
Search Complexity
Time Complexity
If linear search is implemented inside a node, then total complexity is Θ(logt n).
If binary search is used, then total complexity is Θ(log2t.logt n).
B+ Tree Applications
- Multilevel Indexing
- Faster operations on the tree (insertion, deletion, search)
- Database indexing